コラム「法則」
2021/02/15
非営利活動法人 設備システム研究会
三木秀樹
一口に科学技術と言われるが、科学は法則を発見することであり、技術は法則の応用方法を発明することだ。
なので、「科学は役に立たない」としばしば言われるのは、技術が追いついていないせいだ。ご叱責は科学者ではなく、技術者が負うべきものだ。科学者の皆様、ご迷惑をおかけしております。付け加えれば「そんなことも知らないで、科学は役に立たない、なんて言うなよ、このーっ#」。
科学と技術の関係は、知能における学習と推論の関係に似ている。科学は学習に、技術は推論に通じる。学習と推論が相互に影響して知能が発達するように、科学と技術が相互に影響して科学技術が発達する。何だか、美しいなぁ。
でも、科学には自然科学と人文科学がある。自然科学の法則には再現性、つまり同じ条件なら同じ結果を得られるという、とても役に立つ性質があるけど、人文科学はどうなのかな。もし、再現性のある法則がなければ、何の役に立つのかな。あれ?、もしかして「科学は役に立たない」って、人文科学のこと?、なんて言うと、人文科学系の人に叱られるかな。
有名なマーフィーの法則、「If anything can go wrong, it will. (失敗しうるものは、そうなる。)」は自然科学の法則ではなくて、単なるジョークらしい。でも、もう少し丁寧に、例えば、「If anything can go wrong, it will based on its possibility. (失敗しうるものは、その可能性に基づいて、そうなる。)」と言えば、ジョークであっても、正しいはずだ。さらに、「If anything can go right, it will. (成功しうるものは、そうなる。)」とも言えそうだけど、ジョークにはならないなぁ。
写真 私の失敗(設備屋なら分かる)
可能性と言えば、確率と統計の話になる。確率は一種の学習、統計は一種の推論だ。でも、「世の中には3つのウソがある。ウソと大ウソ、そして統計だ。」と言われるほど、アヤシイもののようだ。確率と統計の数学の理屈は正しくても、厳密に適用されないとアヤシクなる。厳密に適用される、とは、たくさん繰り返した時に起こる機会が等しい、という前提条件が守られることだ。架空の世界での理想的な条件下では、コインを投げれば表と裏が出る機会は等しいとしても、現実の世界での理想的でない条件下では、なかなかそうはならない。なのに、現実の世界で、確率的にこうだ、だから統計的にこうだ、と言うからアヤシクなる。タバコを吸うと早死にする、ってのもホントなのかな。
未来予測の法則なんてのもある。もちろん、これも自然科学の法則ではないが、ジョークでもない。未来予測の法則は、生化学分野の科学者であると同時に、著名なSF作家でもあり、『空想自然科学入門』などの科学エッセーの作者でもあるアイザック・アシモフ先生が考えたものだ。
未来予測の法則は、要すれば、未来は過去と現在の延長線上にある、というものだ。例えば、施工図なら、CADで図面を手書きする必要がなくなり、BIMで図面を読み取る必要もなくなった。つまり、過去から現在への流れは、図面を読み書きする労力が減ったということだ。であれば、未来は、図面を考えて作る必要がなくなる、とかね。とゆーことで、やっと「施工図作成の自動化」に辿り着いた。ふぅ。
カーナビや乗換案内は、出発点と到着点を与えると、最短距離(時間)の経路を計算してくれる。この理屈は、昔の私にはブラックボックスだったけど、施工図作成の自動化で経路配置計算をして、同じ理屈だとやっと分かった。これらは全て探索問題で、線(エッジ)と交点(ノード)で構成される探索木を辿りながら、最適な解を見つけるものだ。このとき、単純に総当たりの計算もできるが、探索木が大きくなると計算時間がスゴイことになる。なので、見込みのない解をさっさと捨てるというテクニックを使って、計算時間を短縮する。
出典: Wikipedia
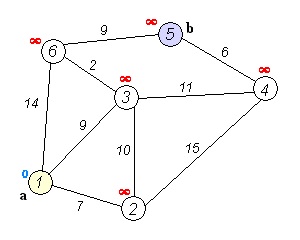
図 探索木
このテクニックの一つがダイクストラ法だ。ダイクストラ法は、計算機科学分野の科学者であると同時に、BASIC言語とGOTO文がキライで、鉄ちゃんでもあるらしいエドガー・ダイクストラ先生が考えたものだ。
でも、ダイクストラ法では線には評価値を与えられるが、交点には与えられない。これだと、配管の長さを評価できても、曲りの数を評価できない。また、ダイクストラ法では正と負の評価値を混在できない。これだと、配管は長くなるけど共通架台を通したい場合を評価できない。とゆーことで、そのままでは経路配置計算には使えない。「じゃあ、どーするんだよ#」とおっしゃるアナタ、続きはシス研のWGで一緒に勉強しない?